Универсальный метод построения структурированных граф-схем алгоритмов был предложен Ашкрофтом и Манной [13,14], который в терминологии [1] по неструктурированной ГСА1 или ГСА2 строит структурированную ГСА4 или ГСА5 с многозначным кодированием состояний.
Однако, по мнению автора, этот метод обладает рядом недостатков, не позволяющих получать хорошо понимаемые граф-схем алгоритмов:
Так как указанный метод предназначен для построения структурированных граф-схем алгоритмов, то из его содержания следует, что если исходная граф-схема уже структурирована, то к ней этот метод применяться не должен. По этой причине, если, например, в качестве исходной задана СГСА2 (рис.3 [1]), то исходя из изложенного она не должна подвергаться дальнейшим преобразованиям. Однако, как показано в [1], эта граф-схема "плохо" понимается и вместо нее для целей общения целесообразно использовать граф-схему алгоритма (рис.10) или граф переходов (рис.11).
Таким образом, в целом идея, предложенная Ашкрофтом и Манной порочна, так как незачем сначала строить неструктурированную граф-схему алгоритма, чтобы потом ее структурировать. Следует либо сразу строить структурированную граф-схему с дешифратором состояний для принятого варианта кодирования, либо, что более целесообразно, производить исходное описание в виде графа переходов для выбранного типа автомата, в котором, по-возможности, должны отсутствовать умалчиваемые значения переменных, и который изоморфно реализуется, например, с помощью управляющей конструкции switch языка Си, производящей одновременно расцикливание и структурирование и обеспечивающей доступ к любому значению многозначной переменной, соответствующей состояниям автомата. Подход применим и для языков низкого уровня, например, языков инструкций программируемых логических контроллеров.
Введение понятия "состояние" делает каждую компоненту программы "наблюдаемой" изнутри (с помощью одной многозначной переменной), а не только по входам и выходам. В получаемые программы легко вносятся изменения. Они достаточно просто проверяются (в качестве теста используется граф переходов) и ввиду изоморфизма с первичным описанием легко верифицируются.
Графы переходов по форме изображения являются в общем случае "существенно плоскостными", что позволяет отражать алгоритмы управления в более естественной форме, чем в виде граф-схемы или диаграммы Графсет [9], которые по стандартам обычно изображаются в форме, приближающейся к "линейной", в направлении сверху вниз. Такая форма представления соответствует последовательному книжному изображению и чтению текстов, но не соответствует плоскостному (параллельному) изображению картин, более удобных для восприятия человеком. При этом, естественно, что графы переходов должны быть в максимальной степени планарными. Графы переходов являются более ранней "сущностью" теории алгоритмизации (теории автоматов) по сравнению с другими, рассмотренными в настоящей работе, и поэтому в соответствии с принципом Оккама [4], по которому "не следует размножать сущности без необходимости", можно утверждать, что для многих задач логического управления такая необходимость не наступает.
При этом отметим также, что графы переходов в отличие от таблиц переходов, оперирующих с минтермами и содержащих обычно большое число пустых клеток, существенно более обозримы и практически применимы для задач большой размерности. Основное достоинство графов переходов, позволяющее описывать задачи такой размерности, состоит в том, что если граф ортогонализован, то переход между двумя вершинами определяется не всеми входными переменными, упоминаемыми в пометках всех дуг графа, как это имеет место при использовании таблиц переходов, а только теми из входных переменных, которые помечают дугу между указанной парой вершин — свойство локальности описания.
При устранении противоречий не ортогонализацией, а расстановкой приоритетов, умолчание обозначений некоторых входных переменных ухудшает читаемость графов переходов, так как для дуг с меньшими приоритетами, исходящих из некоторой вершины, не удается сразу определить (прочесть) перечень всех переменных, от которых зависит каждый переход по этим дугам. Для определения указанного перечня в этом случае приходится анализировать пометки всех дуг, исходящих из рассматриваемой вершины — локальность описания уменьшается.
Проблемы, возникающие для задач большой размерности при использовании таблиц переходов как основной модели, для которой разработаны алгоритмы теории автоматов при двоичной аппаратной, и в особенности, асинхронной реализации, видимо, явились тем сдерживающим фактором, который по традиции распространился и на диаграммы переходов (основное название графов переходов в теории автоматов), являющиеся в теории автоматов вспомогательной (иллюстрационной) моделью, и не позволил до настоящего времени широко применять графы переходов в качестве языка общения и спецификации при программной реализации задач логического управления, при которой традиционные задачи теории автоматов либо отсутствуют либо не являются определяющими.
По мнению автора, при современном уровне развития элементной базы при программной реализации практических задач логического управления основным критерием построения программ должна являться их хорошая читаемость и как следствие безошибочность, а остальные критерии должны быть вспомогательными (хотя в программируемых логических контроллерах их ограниченные ресурсы могут определять выбор моделей в процессе алгоритмизации). Поэтому автор надеется, что настоящая работа позволит графам переходов занять подобающее им место при программной реализации рассматриваемого класса задач.
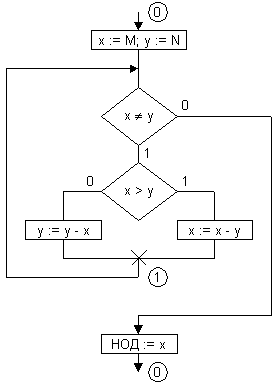
Предлагаемый подход может быть использован не только для логико-временных алгоритмов управления, но и для логико-вычислительных алгоритмов. На рис.27 в качестве примера приведена ГСА1, реализующая алгоритм определения наибольшего общего делителя двух целых положительных чисел M и N (алгоритм Евклида).

Рис. 27.
Эта граф-схема алгоритма является не автоматной, а логико-вычислительной. Она может программироваться с помощью подхода предлагаемого в настоящей работе по графу переходов, описывающему логико-вычислительный процесс и являющемуся автоматом Мили с флагами (рис.28).
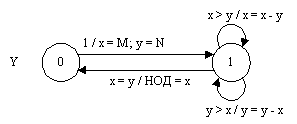
Рис. 28.
Необходимо отметить, что этот граф переходов существенно компактнее, чем соответствующая граф-схема алгоритма.
Предлагаемый подход, по мнению автора, может представлять интерес для специалистов по объектно-ориентированному программированию в качестве математического аппарата для работы с "состояниями", введенными для описания "объектов".