УНИВЕРСИТЕТ ИТМО
Кафедра «Технологии программирования»

Использование граф-схем и графов переходов при программной реализации алгоритмов логического управления. Часть 2

Отсюда можно скачать полный текст обеих частей статьи в формате pdf (354 кб)

(©) 1996 А.А.Шалыто

Федеральный научно-производственный центр ГУП "НПО "Аврора"",
Санкт-Петербургский государственный институт точной механики и оптики
(технический университет)

Статья опубликована журнале "Автоматика и телемеханика", 1996. N6, C.148-158; N7, С.144-169.

Имеется английская версия: Shalyto A.A. Algorithmic graf schemes and transition graphs:
their application in software realization of logical control algorithms.
//Automation and Remote Control. 1996. N6, P.890-897; N7, P.1027-1045.

УДК 519.714

1. Введение

В [1] рассмотрены особенности граф-схем алгоритмов (ГСА) и программ, затрудняющие их понимание. Предложена классификация граф-схем алгоритмов и показано, что переход к графам переходов, удовлетворяющим определенным условиям, позволяет решить проблему чтения и понимания спецификаций.

Настоящая работа посвящена описанию методов построения понимаемых графов переходов по граф-схемам алгоритмов и решению обратной задачи — построению понимаемых граф-схем алгоритмов по графам переходов. Излагаются методы программирования, обеспечивающие для языков различных уровней понимаемость программ, реализующих функциональные задачи логического управления. Выполнено сравнение предлагаемого подхода с основным методом структурного программирования — методом Ашкрофта и Манны.

2.Метод построения читаемого графа переходов по граф-схеме алгоритма с обратными связями

Изложение метода выполним на примере. Пусть задана граф-схема алгоритма с внутренними обратными связями (ГСА1 в терминологии [1]), представленная на рис.1, и требуется понять эту граф-схему.

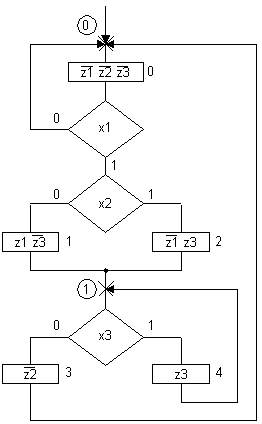
Рис. 1.

Если закодировать числами (числа в кружках) точку начала и конца (если она имеется), а также точки, следующие за операторными вершинами, и определить пути в граф-схеме алгоритма между смежными точками [2], то можно построить граф переходов автомата Мили с неоднозначными значениями выходных переменных (рис.2), число вершин в котором равно количеству точек, введенных в граф-схему.

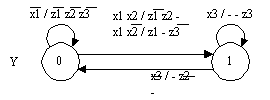
Рис. 2.

Этот граф переходов может быть эффективно запрограммирован, например, на языке Си, но понять (из-за умолчаний некоторых значений выходных переменных) как он функционирует и соответственно как функционирует ГСА1 весьма сложно.

Поэтому построим по ГСА1 граф переходов автомата Мура, который по принципам построения должен пониматься лучше [1]. Для этого закодируем числами (без кружков) каждую операторную вершину (рис.1) и определим все пути между смежными вершинами [2]. Используя эту информацию, построим граф переходов автомата Мура с неоднозначными значениями выходных переменных, содержащий пять вершин, закодированных многозначными (десятичными) числами (рис.3).

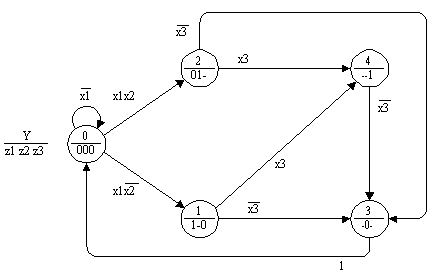
Рис. 3.

Этот граф понимается лучше, чем предыдущий, но также весьма сложно, так как и этот граф переходов содержит умолчания.

Анализируя значения, формируемые при прохождении различных путей в этом графе переходов, построим по результатам анализа граф переходов автомата Мура без умолчаний с девятью вершинами (рис.4).

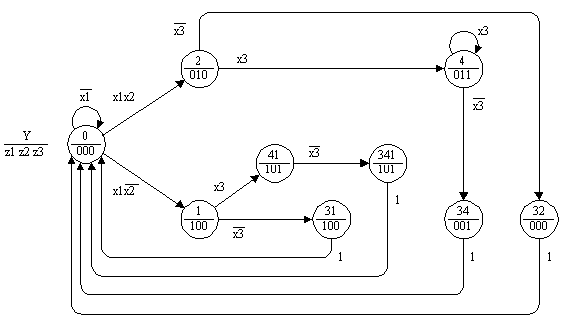
Рис. 4.

Так как в этом графе переходов в каждой паре вершин (41, 341) и (1, 31) формируются одинаковые значения выходных переменных, то вторые вершины в этих парах вместе с дугами, помеченными единицами (безусловные переходы), могут быть исключены. При этом первые вершины этих пар соединяются с нулевой вершиной. С этой же вершиной соединяется вершина 2, так как вершина 32, в которой формируются те же значения выходных переменных, что и в нулевой вершине, может быть исключена. Получающийся при этом граф переходов автомата Мура содержит шесть вершин (рис.5).

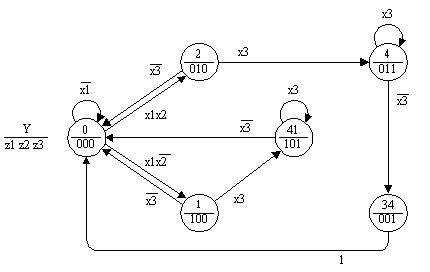
Рис. 5.

Этот граф переходов "абсолютно" понятен, так как он компактен и при его чтении не требуется помнить предысторию. При этом необходимо отметить, что его структура в отличие от ранее рассмотренных графов переходов (рис.2, 3) существенно отличается от исходной граф-схемы.

Полученный граф переходов полон и непротиворечив, однако содержит, как и ГСА1, два генерирующих контура 0-1 и 0-2, устраняя которые, например введением переменной x3 в пометку дуг 0-1 и 0-2, получим корректный граф переходов (рис.6). В этом графе не изменяющиеся значения выходных переменных перечеркнуты.

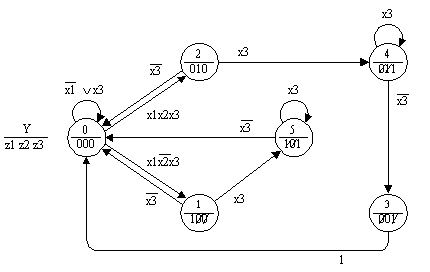
Рис. 6.

Обратим при этом внимание на тот факт, что в граф переходов указанные изменения были внесены весьма просто без корректировки его структуры, в то время как для граф-схемы алгоритма это потребовало бы существенных изменений схемы, что может приводить к ошибкам.

Из изложенного следует, что именно граф переходов (рис.6), а не ГСА1, и должен использоваться в качестве "предмета обсуждения" с Заказчиком и спецификации на программирование при отсутствии жестких ограничений на объем памяти программ. Приведенный граф переходов в отличие от ГСА1 описывает поведение автомата в явной и понятной форме и содержит достаточно информации, чтобы быть формально реализованным с помощью различных алгоритмических моделей (системой булевых формул, функциональной схемой, ГСА4 [1] и т.д.) [3, 4].

Каждая из этих алгоритмических моделей, в свою очередь, может быть изоморфно отражена программной моделью, однако степень изоморфизма последней с графом переходов различна. Действительно, если тексты программ, записанные, например на языке Си, формально построенные по системе булевых формул или функциональной схеме, функционально эквивалентны графу переходов, то внешне эти тексты на граф переходов непохожи, особенно для системы булевых формул, описывающей функциональную схему с триггерами. При этом отметим, что эта система булевых формул отличается от системы таких формул, построенной непосредственно по графу переходов. С другой стороны, в состав указанного языка входит такая управляющая конструкция как переключатель (switch), при использовании которой удается обеспечить изоморфизм между текстом программы и графом переходов, что открывает возможность простого чтения не только спецификаций, но и текстов программ.

В заключение раздела отметим, что, если для построения некоторых алгоритмических и программных моделей, например системы булевых формул или функциональной схемы, вся информация, приведенная на рис.6 необходима, то при использовании управляющей конструкции switch в графе переходов пометки петель могут умалчиваться (предполагая, что в каждой вершине обеспечивается логическая полнота пометок дуг, исходящих из нее), а вместо ортогонализации этих пометок могут расставляться приоритеты, указываемые на дугах штрихами, число которых тем меньше, чем выше номер приоритета (рис.7).

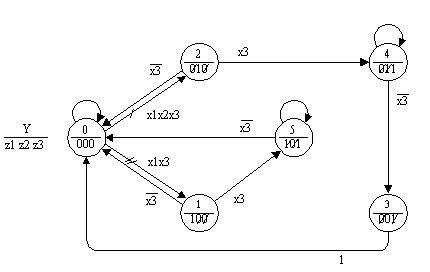
Рис. 7.

Это в общем случае позволяет резко упростить граф переходов и уменьшить объем программы, практически без ухудшения их понимаемости.

Перейдем к рассмотрению вопроса о построении читаемой граф-схемы алгоритма без внутренних обратных связей по графу переходов без умолчаний. В [1] было показано, что "плохо организованные" граф-схемы алгоритмов без внутренних обратных связей (ГСА2 в терминологии [1]) весьма трудно читаются. Покажем какой структурой должны обладать граф-схемы этого класса, чтобы устранить указанный недостаток.