УНИВЕРСИТЕТ ИТМО
Кафедра «Технологии программирования»

Использование граф-схем и графов переходов при программной реализации алгоритмов логического управления. Часть 2

12. Программирование граф-схем алгоритмов и графов переходов с многозначным кодированием состояний в базисе языков низкого уровня

Как отмечалось в [1], для учета свойств управляющих конструкций используемого языка программирования целесообразно переходить от исходной граф-схем алгоритма к тексту программы не непосредственно, а используя промежуточную форму граф-схем алгоритма (ГСА3 в терминологии [1]).

На рис.25 приведена граф-схем алгоритма, линеаризованная и структурированная специальным образом (все условные вершины в каждом блоке при не выполнении условия передают управление в одну точку), эквивалентная граф-схеме алгоритма (рис.19).

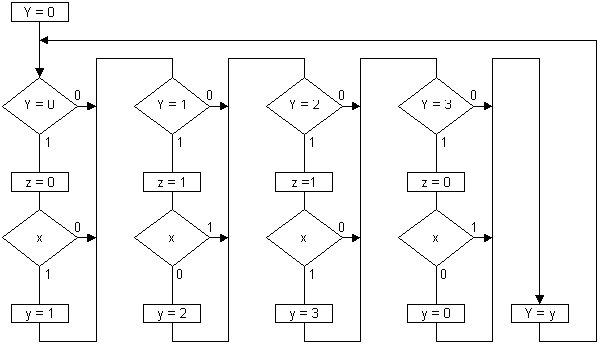
Рис. 25.

Полученная граф-схема алгоритма, в свою очередь, может быть практически изоморфно преобразована в граф-схему программы, учитывающую семантику применяемых команд и архитектурные особенности используемого вычислительного устройства, например программируемого логического контроллера [12], по которой также изоморфно может быть построен текст программы на языке инструкций этого контроллера:

STR R C 0 ; Ввод константы 0 в регистровый сумматор (РС:=0)
EQU R M Y ; if(Y=0) битовый сумматор (БС)=1
IF T ; if(БС) перейти к следующей команде, иначе на метку CONT
EQ RO z ; if(БС) z=0
IF I x ; if(x) перейти к следующей команде, иначе на метку CONT
STR R C 1 ; РС:=1
EQ R SM y ; if(БС) у=1CONT ; переход к следующей команде
STR R C 1
EQU R M Y
IF T
EQ SO z
IF I x
STR R C 2
EQ R SM y
  ...
STR R M y; РС:= y
EQ R M Y; Y := РС
STOP ; передача управления в начало программы

Если в качестве языка спецификации в этом случае использовать не граф-схему алгоритма, а граф переходов (рис.7 [1]), то последний может быть практически изоморфно отражен в следующий текст программы:

STR R C 0 ; Ввод константы 0 в регистровый сумматор (РС:=0)
EQU R M Y ; if(Y=0) битовый сумматор (БС)=1
EQ RO z ; if(БС) z=0
AND I x ; БС:=БС&x
STR R C 1 ; РC:=1
EQ R SM y ; if(БС) y=1
STR R C 1 ; РС:=1
EQU R M Y ; if(Y=1) БС=1
EQ SO z ; if(БС) z=1
AND NI x ; БС:=БС&!x
STR R C 2 ; РС:=2
EQ R SM y ; if(БС) y=2
  ...
STR R M y ; РС:=y
EQ R M Y ; Y:=РС
STOP ; передача управления в начало программы

Эта программа содержит меньшее число команд по сравнению с предыдущей. Она не включает условных переходов и выполняется в режиме последовательного выполнения всех команд и поэтому может быть еще более упрощена за счет исключения третьей команды, если заменить девятую команду на команду EQ O z (z:=БС) при условии, что в начале программы z = 0. Это объясняется тем, что в этом случае пока автомат находится в первой вершине в ячейку z записывается единица и ноль, когда он "уходит" из этой вершины. Дальнейшее упрощение программы связано с еще более значительным уменьшением степени ее изоморфизма с графом переходов. При этом каждая пара команд 5-6 и 11-12 может быть заменена командой INC R M y (y:=y+1).

Рассмотренные программы обеспечивают реализацию за один программный цикл не более одного блока в граф-схеме алгоритма (рис.19) или одного перехода в графе переходов (рис.7 [1]) за счет использования второй многозначной внутренней переменной y, в которой присваивается значение Y на время одного программного цикла.

При этом необходимо отметить, что одной дополнительной переменной y достаточно для реализации любой системы взаимосвязанных графов переходов. Если отказаться от требования, чтобы за один проход выполнялось не более одного перехода в графе переходов, то граф-схема (рис.25) может быть преобразована в граф-схему алгоритма (рис.26).

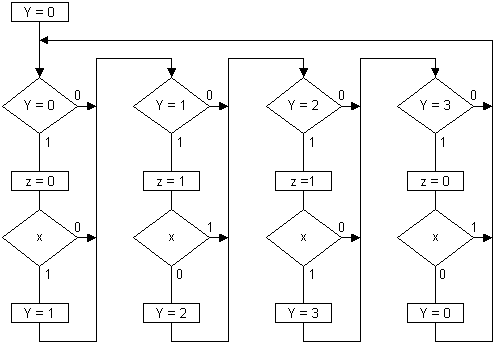
Рис. 26.

Это позволяет еще более упростить приведенные выше программы. Построенная граф-схема алгоритма корректна, так как в программируемом логическом контроллере [12] в течение одного прохода программы значения введенных входных переменных не изменяются.

Если в качестве языка спецификации использовать граф переходов и снять ограничение на число переходов, реализуемых за один программный цикл, то появляется возможность применения при написании программы такой нетрадиционной управляющей конструкции как шаговый регистр, существующей в системах команд многих программируемых логических контроллеров [9,12]. Однако в этих работах шаговый регистр предлагается использовать в режиме формирования последовательных шагов и не упоминается возможность применения его для реализации произвольных автоматов. Поэтому настоящую работу можно считать в качестве обоснования такой возможности.

Приведем в качестве примера программу, реализующую граф переходов (рис.7 [1]), в которой используется нулевой (из 32 имеющихся) шаговый регистр, находящийся в начальный момент времени на нулевом (из 256 допустимых) шаге (в нулевом состоянии):

READ S 0 ; Выбор в качестве рабочего шагового регистра с номером 0

STR S 0 ; if(S=0) БС=1
EQ RO z ; if(БС) z=0
AND I x ; БС:=БС&x
STEP S 1 ; if(БС) S=1
STR S 1 ; if(S=1) БС=1
EQ SO z ; if(БС) z=1
AND NI x ; БС:=БС&!x
STEP S 2 ; if(БС) S=2  ...
STOP

Так как и эта программа не содержит условных переходов, то и в ней третья команда может быть исключена при замене седьмой команды на команду EQ O z при условии, что в начальный момент времени z = 0.

Подходы, изложенные в настоящем разделе, могут быть использованы и для автоматов Мили, смешанных автоматов и автоматов с флагами. Так, например, граф переходов автомата Мили (рис.8 [1]), описываемый на языке Си следующей программой:

Y=0;
M : 
  if((Y==0)&x) {z=0; Y=1;}
  if((Y==1)&!x) {z=1; Y=2;} 
  if((Y==2)&x) {z=1; Y=3;}
  if((Y==3)&!x) {z=0; Y=0;}
goto M;

реализуется следующей программой, использующей шаговый регистр:

READ S 0
STR S 0
AND I x
EQ RO z
STEP S 1
STR S 1
AND NI x
EQ SO z
STEP S 2
  ... 
STOP

Из изложенного следует, что использование шаговых регистров делает программирование автоматов на языке инструкций весьма высокоуровневым. Эта же тенденция сохраняется и при реализации управляющих автоматов, тем более, что в ряде случаев функциональные элементы задержки могут быть реализованы командой NEXT Si D, которая, если шаговый регистр находится на шаге с номером i в течение D секунд, обеспечивает переход на шаг с номером i + 1. При применении этой команды может возникнуть необходимость в преобразовании исходного графа переходов (за счет увеличение числа вершин в нем) для обеспечения перехода только в соседнюю вершину по истечении выдержки времени. При этом необходимо отметить, в данном случае управляющий автомат не декомпозируется на автомат и функциональные элементы задержки, а программируется как единое целое. Реализуем в качестве примера граф переходов автомата Мура с флагом (рис.11 [1]), предварительно увеличив число вершин в нем до пяти, и при условии, что в начале программы z1 = z2 = 0 :

READ S 0
IF S 0
STR M x1
STEP S 1
STR I x0
EQ SM x1
STEP S 2
CONT
STR S 1
EQ O z2
NEXT S1 D
STR S 2
AND NM x1
STEP S 3
STR S 3
EQ O z1
NEXT S3 D
STR S 4
STEP S 0
STOP

В этой программе изоморфизм с графом переходов обеспечивается по вершинам последнего. При этом фрагмент программы, соответствующий дуге с большим приоритетом, исходящей из нулевой вершины, расположен ниже фрагмента, соответствующего дуге с меньшим приоритетом, исходящей из этой вершины. Так как в этой программе команды выдачи значений выходных переменных входят только в "линейный" участок (не "защищены" командой if), то команды формирования их нулевых значений не применяются, а получение единичных значений выполняется командами EQ O zi.

Если изоморфизм обеспечивать не по вершинам графа переходов, а по его дугам, то фрагмент программы, соответствующий дуге с большим приоритетом, размещается выше фрагмента, соответствующего дуге с меньшим приоритетом:

READ S 0
STR S 0
AND I x0
EQ SM x1
STEP S 2
STR S 0
AND M x1
STEP S 1
STR S 1
EQ O z2
NEXT S1 D
STR S 2
AND NM x1
STEP S 3
STR S 3
EQ O z1
NEXT S3 D
STR S 4
STEP S 0
STOP