Использование многозначного кодирования позволяет для ГСА4, также как и для графов переходов, изоморфно переходить к текстам программ, минуя построение промежуточных граф-схем [1]. При этом несмотря на то, что графы переходов содержат петли и контура (негенерирующие), их не приходится принудительно расцикливать и структурировать, а эти проблемы решаются при программировании выбором соответствующей управляющей конструкции.
Наиболее просто это достигается при использовании такой управляющей конструкции, как например, оператор switch языка Си [5, 6, 10]. Приведем в качестве примера программу, использующую этот оператор для реализации графа переходов автомата Мура (рис.7 [1]) и граф-схемы алгоритма (рис.19):
switch (Y)
{
case 0 :
z=0;
if(x) Y=1;
break;
case 1 :
z=1;
if(!x) Y=2;
break;
case 2 :
/* z=1; */
if(x) Y=3;
break;
case 3 :
z=0;
if(!x) Y=0;
break;
}
Приведенная программа обладает замечательным свойством — она с гарантией делает только то, что описывает граф переходов и не делает ничего лишнего, что легко проверяется сверкой текста программы с графом переходов, так как при безошибочном переходе от графа переходов к программе должен быть обеспечен их полный изоморфизм. Этим свойством обладают не все алгоритмические модели. Так, например, если автомат с s состояниями реализуется системой m булевых формул (m = ]log2 s[), а s != 2m , то система реализует другой автомат с числом состояний 2m , в котором исходный автомат является лишь ядром построенного, а переходы из новых 2m -s состояний в заданные зависят от принятого варианта доопределения.
В приведенной программе в состоянии 2 (case 2) значение выходной переменной, не изменяющееся при переходе из предыдущего состояния, закомментировано. Это, с одной стороны, уменьшает объем памяти, а с другой — сохраняет хорошую читаемость программы. В этой программе каждый оператор break осуществляет передачу управления за закрывающуюся фигурную скобку, что при невыполнении условия в операторе if сохраняет предыдущее состояние, а при его выполнении — не позволяет выполнить более одного перехода в графе переходов. При этом для системы взаимосвязанных графов переходов за один программный цикл в каждом графе реализуется не более одного перехода. Это делает доступным номер любого состояния рассматриваемого автомата для других компонент алгоритма управления вне зависимости от значений входных переменных, в отличие, например, от ГСА2 (рис.3 [1]), в которой при x1 = x2 = 1 значение z = 1 для других компонент недоступно.
Так, например, если первая компонента алгоритма управления реализована указанным образом и значение переменной Y1 равное шести доступно другим компонентам, то фрагменту системы взаимосвязанных графов переходов (рис.20) соответствует следующий фрагмент программы, использующий значение шестого состояния первой компоненты в качестве условия перехода в двух других компонентах:
switch (Y2)
{
...
case 1 :
if(Y1==6) Y2=3;
...
}
switch (Y3)
{
...
case 4 :
if(Y1==6) Y3=5;
...
}
Из изложенного следует весьма неприятный факт, состоящий в том, что особенности программной реализации влияют не только на чтение текста программы, но и на чтение спецификации — графа переходов или системы взаимосвязанных графов переходов. Для обеспечения универсальности, в том числе и для графов переходов с неустойчивыми вершинами, целесообразно считать, что в каждом графе переходов за один проход выполняется не более одного перехода, что на программном уровне поддерживается указанным образом.
Приведем теперь пример программы, построенной по графу переходов автомата Мура (рис.8 [1]) и ГСА4 (рис.21), предполагая, что в начале Y = 0; z = 0:
switch (Y)
{
case 0 :
if(x) { z=1; Y=1; }
break;
case 1 :
if(!x) {/* z=1; */ Y=2;}
break;
case 2 :
if(x) { z=0; Y=3;}
break;
case 3 :
if(!x) {/* z=0; */ Y=0;}
break;
}
С помощью управляющей конструкции switch также эффективно реализуются и смешанные автоматы.
Из изложенного следует, что граф переходов, во-первых, может одновременно использоваться в качестве спецификации как алгоритма управления, так и программы, а, во-вторых, с помощью управляющей конструкции switch он изоморфно отражается в текст структурированной программы, которая может быть наблюдаемой не только по двоичным выходам, но и, что самое главное, по десятичному номеру состояния. При этом для проверки программы на экран дисплея для каждого графа переходов автомата Мура, Мили или смешанного автомата достаточно вывести только одну десятичную внутреннюю переменную (сигнатуру). Это позволяет при исследовании поведения автомата в динамике следить только за значениями этой переменной (предварительно определив, например, для автомата Мура, соответствие между номером состояния и значениями выходных переменных в этом состоянии), а не за многими двоичными внутренними переменными как это делается при традиционном подходе.
Это позволяет ввести в программирование понятие "наблюдаемость" по аналогии с понятием "измеримость" (по Л.Заде), используемым в автоматическом управлении [11].
Получаемые таким образом программы обладают высокой модификационной способностью (в некотором смысле легко управляемы) и хорошо читаются при условии, что значения выходных переменных задаются однозначно, так как в этом случае они не зависят от предыстории. Графы переходов автоматов с флагами также изоморфно отражаются в текст программы с помощью управляющей конструкции switch. Однако зависимость следующего состояния от предыстории резко уменьшает их модификационную способность. Отметим также, что основная причина простоты внесения изменений в программы, построенные указанным образом по графу переходов, состоит в том, что в последних вершины связаны между собой непосредственно в отличие от граф схем, в которых операторные вершины в общем случае соединены через условные вершины и поэтому изменение в одном переходе оказывает существенное влияние на другие переходы. При использовании предлагаемого подхода верификация программы может производиться сверкой текста программы с графом переходов. Для однокомпонентных алгоритмов управления граф переходов может использоваться в качестве теста для проверки программы, а для многокомпонентных алгоритмов управления (по аналогии с сетями Петри) по системе взаимосвязанных графов переходов должен строиться граф достижимых маркировок, позволяющий исследовать все функциональные возможности системы и представить ее поведение одним графом переходов. Эта задача практически разрешима при отсутствии параллелизма по состояниям в алгоритме управления или для задач малой размерности. Для независимых параллельных процессов строить единый граф переходов нет необходимости, так как они могут проверяться по отдельности.
Подход, излагаемый в настоящей работе, позволяет предложить метод программирования граф-схем алгоритмов с внутренними обратными связями, которые в многозадачном режиме использования применяемого вычислительного устройства не реализуется традиционным путем без предварительного расцикливания [1].
Суть предлагаемого метода состоит в том, что по заданной граф-схеме алгоритма строится эквивалентный граф переходов, который затем изоморфно отражается в текст программы с помощью управляющей конструкции switch.
Пусть, например, задана граф-схема алгоритма с внутренними обратными связями (рис.1). По этой граф-схеме может быть построен граф переходов автомата Мили (рис.2) или граф переходов автомата Мура (рис.3), каждый из которых может быть однозначно реализован управляющей конструкцией switch. Несмотря на то, что получающиеся при этом программы весьма компактны, эти графы переходов содержат генерирующие контура и их понимание весьма затруднительно из-за неоднозначности значений выходных переменных. Эти недостатки отсутствуют в программе, построенной по преобразованному графу переходов автомата Мура (рис.7):
switch (Y)
{
case 0 :
z1=0; z2=0; z3=0;
if(x1&x3) Y=1;
if(x1&x2&x3) Y=2;
break;
case 1 :
z1=1; /*z2=0; z3=0;*/
if(!x3) Y=0;
if(x3) Y=1;
break;
case 2 :
/*z1=0;*/ z2=1; /*z3=0;*/
if(!x3) Y=0;
if(x3) Y=4;
break;
case 3 :
/*z1=0;*/ z2=0; /*z3=1;*/
Y=0;
break;
case 4 :
/*z1=0; z2=1;*/ z3=1;
if(!x3) Y=3;
break;
case 5 :
/*z1=1; z2=0;*/ z3=1;
if(!x3) Y=0;
break;
}
Число строк в этой программе равно s + d + 1, где d — число дуг (включая петли) в графе переходов. В метке case 0 оператор if, соответствующий дуге с наибольшим приоритетом, исходящей из вершины 0, размещается ниже оператора if, соответствующего дуге с меньшим приоритетом. При такой программной реализации проблемы расцикливания и структурирования исходной граф-схемы решаются автоматически в ходе построения программы. При этом отметим, что построение графа переходов по граф-схеме алгоритма с внутренними обратными связями не является необходимым. Для написания программы в этом случае достаточно выполнить многозначное кодирование (раздел 2) операторных вершин заданной граф-схем алгоритма (для построения программы, соответствующей автомату Мура) или точек, следующих за операторными вершинами (для построения программы, соответствующей автомату Мили). Быстродействие программы может быть повышено при усложнении ее структуры:
switch (Y)
{
case 0 :
z1=0; z2=0; z3=0;
if(x1&x2&x3) { Y=2; break; }
if(x1&x3) Y=1;
break;
case 1 :
z1=1; /*z2=0; z3=0;*/
if(!x3) Y=0;
if(x3) Y=1;
break;
case 2 :
/*z1=0;*/ z2=1; /*z3=0;*/
if(!x3) Y=0;
if(x3) Y=4;
break;
case 3 :
/*z1=0;*/ z2=0; /*z3=1;*/
Y=0;
break;
case 4 :
/*z1=0; z2=1;*/ z3=1;
if(!x3) Y=3;
break;
case 5 :
/*z1=1; z2=0;*/ z3=1;
if(!x3) Y=0;
break;
}
В этой программе фрагмент, соответствующий дуге с большим приоритетом, исходящей из нулевой вершины, располагается выше фрагмента, соответствующего дуге с меньшим приоритетом, исходящей из той же вершины.
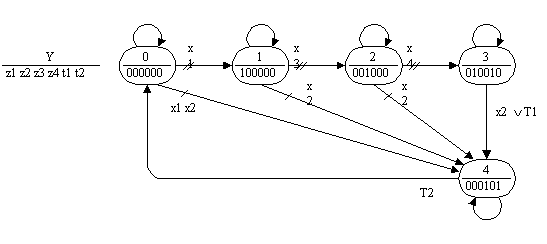
В качестве второго примера рассмотрим граф-схему алгоритма с внутренними обратными связями (рис.2 [1]) и построим эквивалентный ей граф переходов автомата Мура (рис.24).

Рис. 24.
В этом графе переходов, входящем в состав управляющего автомата, каждой единице на позициях t1 и t2 соответствует обращение к процедуре time(i,D), где D — время задержки i-го функционального элемента задержки. Этот граф переходов, также как и предыдущий, реализуется с помощью конструкции switch.