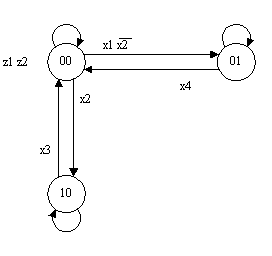
Пусть задан граф переходов автомата без выходного преобразователя с принудительным кодированием состояний (рис.8), в котором при импульсных переменных x1 и x2 генерирующие контура отсутствуют.

Рис. 8.
Кодирование названо принудительным, так как коды, определяющие состояния, совпадают со значениями выходных переменных, формируемых в соответствующих состояниях (вершинах). Этот вид кодирования использован ввиду того, что в рассматриваемом графе переходов комбинации значений выходных переменных во всех вершинах различны. Этот граф переходов предлагается реализовать ГСА4 [1] (рис.9), тело которой состоит из трех слоев.
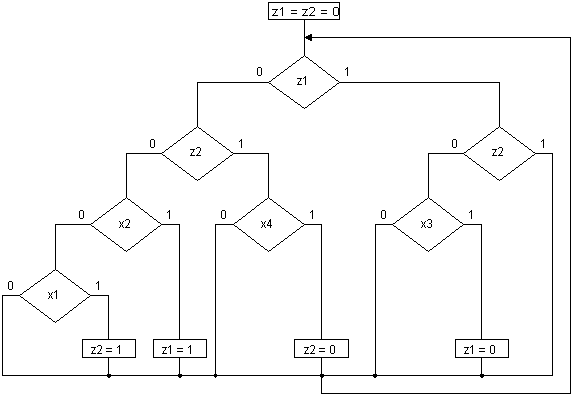
Рис. 9.
Первый из них содержит условные вершины, помеченные переменными z1 и z2, и является дешифратором состояний. Второй слой образован условными вершинами, помеченными входными переменными, и реализует функции переходов автомата. Третий слой содержит операторные вершины, в которых указаны значения выходов, совпадающие в данном случае с кодами следующих состояний.
Несмотря на то, что в операторных вершины этой граф-схемы используются умолчания, она достаточно хорошо понимается, так как в этом случае, в отличие от ГСА2, сохраняемые значения нет необходимости помнить, а их можно определить, "поднимаясь" вверх по соответствующему пути в граф-схеме.
Понимаемость этой граф-схеме придает также и то, что она обладает в отличие, например от ГСА2 (рис.2 [1]), глубиной, определяемой только одним переходом в графе переходов, что является чрезвычайно важным и полезным свойством этого класса граф-схем. Кроме того в этой граф-схеме за один проход в отличии от граф-схемы (рис.3 [1]) не приходится неоднократно пересчитывать значения ни одной выходной переменной, а в отличие от граф-схемы (рис.5 [1]) — многократно проверять значения одной и той же входной переменной. Эта граф-схема не только структурирована в традиционном понимании, но и хорошо организована в том смысле, что условные вершины с пометками Z и X не перемешаны между собой и с операторными вершинами.
Такая организация граф-схем алгоритмов (настоящее состояние — условие перехода — следующее состояние) соответствует нормальному человеческому поведению, при котором, например, просыпаясь утром, человек сначала определяет свое внутреннее состояние (жив-мертв, здоров-болен) и лишь потом "опрашивает" значения входных переменных (например, тепло или холодно на улице), а затем в зависимости от значений этих переменных переходит в следующее состояние (например, одевается соответствующим образом). Ясно, что в этом случае поведение без учета внутреннего состояния только по значениям входных переменных будет выглядеть странным.
Однако при алгоритмизации с помощью граф-схем алгоритмов без внутренних обратных связей понятие "состояние" обычно в явном виде не используется и ее строят, начиная с опроса входных переменных, и в зависимости от их значений формируют те или иные значения выходных, а возможно, и дополнительно введенных внутренних переменных, которые определяют состояния косвенным (компонентным) способом.
Например, несмотря на то, что ГСА2 (рис.3 [1]), реализующая R-триггер, идеально соответствует принципам структурного программирования, она обладает двумя недостатками, затрудняющими ее чтение: пересчет значения z при x1 = x2 = 1 и отсутствие в модели указания в явном виде значения z при x1 = x2 = 0. Этих недостатков лишена граф-схема алгоритма с дешифратором состояний (рис.10), которая, несмотря на большую сложность по сравнению с граф-схемой (рис.3 [1]), понимается лучше.
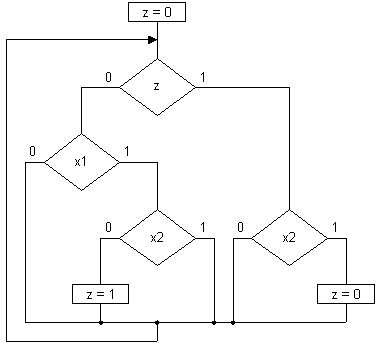
Рис. 10.
Простоту чтения и компактность изображения совмещает в себе граф переходов (рис.11), который при программировании с помощью конструкции switch может быть еще более упрощен (умолчание пометок петель).
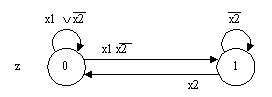
Рис. 11.
Пусть требуется реализовать счетный триггер, поведение которого описывается графом переходов (рис.12).
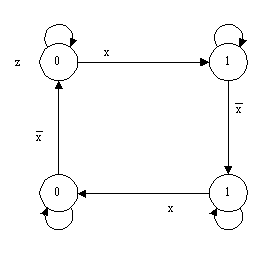
Рис. 12.
Для того, чтобы различать вершины графа переходов, используем принудительно-свободное кодирование состояний автомата, введя отсутствующую в алгоритме управления внутреннюю переменную y (рис.13).
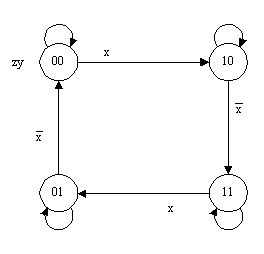
Рис. 13.
Название этого вида кодирования определяется тем, что значения части разрядов кода принудительно задаются значениями выходных переменных z, а значения остальных разрядов, обозначаемых переменными y, могут быть выбраны при программной реализации свободно (произвольно). На рис.14 приведена граф-схема алгоритма, эквивалентная этому графу переходов.
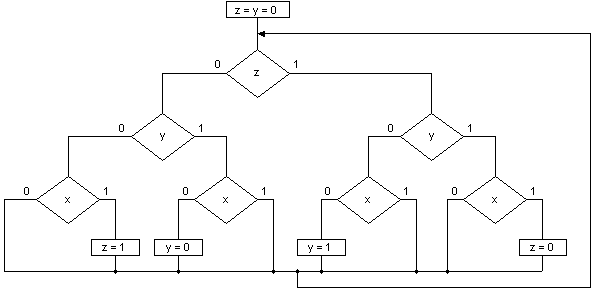
Рис. 14.
Зависимость состояний автомата от значений выхода z в рассмотренных граф-схем алгоритмов (рис.9, 10 и 14) может создать трудности при условии, что эти значения могут изменяться в других компонентах алгоритма управления. Поэтому сделаем независимыми состояния автомата от его выходных значений, перейдя к модели автомата Мура.
На рис.15 приведен граф переходов автомата Мура, реализующий счетный триггер, для рассматриваемого варианта кодирования, а на рис.16 — соответствующая ему граф-схем алгоритма.
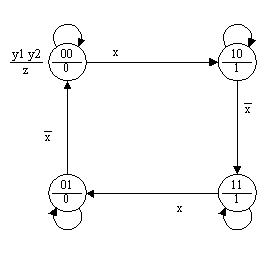
Рис 15.
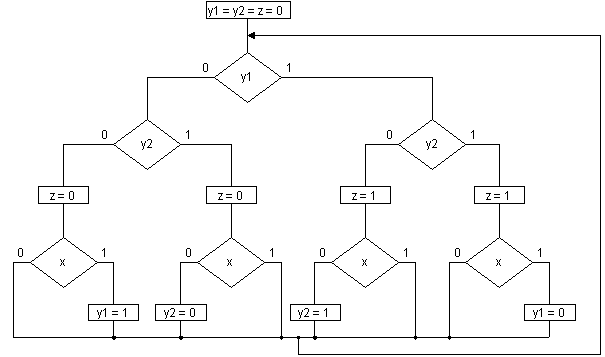
Рис. 16.
Тело этой граф-схемы является четырехслойным (дешифратор состояний, формирование значений выходов, реализация функций переходов, формирование следующего состояния). Недостатки этой граф-схемы состоят в значительной глубине пирамидального дешифратора и большом числе вновь вводимых переменных yi, где 0 < i < ]log s[ - 1; s — число состояний автомата. Первый из этих недостатков устраняется в разд. 6, а оба недостатка — в разд. 7.
Такой вариант кодирования вершин графа переходов автомата Мура (рис.17), названный в [2] единичным (в j-ой вершине графа переходов только битовая переменная yj принимает значение равное единице, а в остальных вершинах значение этой переменной равно нулю), позволяет использовать в граф-схеме алгоритмов (рис.18) линейный дешифратор состояний вместо пирамидального, который применялся в граф-схемах алгоритмов автоматов Мура при других видах кодирования. Недостаток граф-схемы в этом случае состоит в еще большем (по сравнению с предыдущим случаем) числе вновь вводимых битовых переменных yj (0 < j < s - 1), каждую из которых приходится не только устанавливать, но и принудительно сбрасывать.
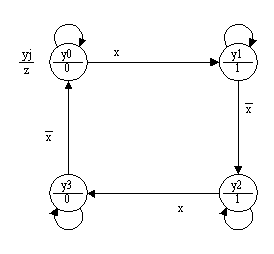
Рис. 17.
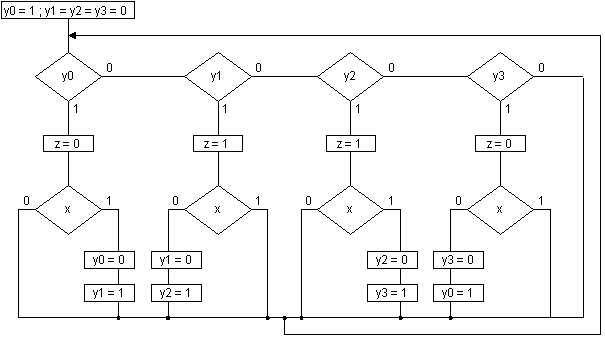
Рис. 18.
Все недостатки предыдущих вариантов кодирования устраняются при переходе к многозначному кодированию состояний автоматов [5, 6]. При этом для автоматов Мура, Мили и смешанных автоматов, реализуемых в виде одной компоненты, для кодирования состояний достаточно иметь одну переменную Y значности s, которую не требуется принудительно сбрасывать, так как она автоматически сбрасывается при переходе от одного значения к другому. При этом для реализации N-компонентного алгоритма управления (реализуемого N графами) с помощью указанных классов автоматов требуется N многозначных переменных Yj, где j=0,..., N-1. Этот вариант кодирования, практически нереализуемый при аппаратной реализации автоматов, по мнению автора, при отсутствии жестких ограничений на объем памяти программ и возможности работы с многозначными переменными должен стать основным при программной реализации автоматов.
На рис.19 в качестве примера приведена граф-схема алгоритма для рассматриваемого варианта кодирования, построенная по графу переходов автомата Мура счетного триггера (рис.7 [1]).
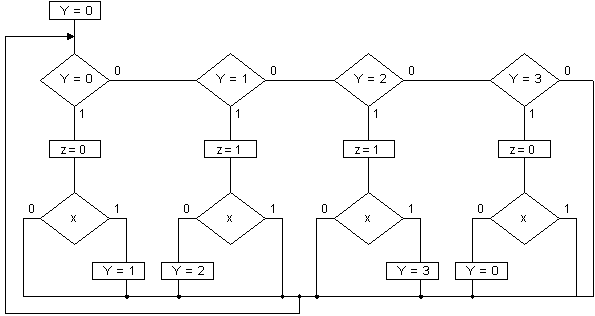
Рис. 19.
В этой граф-схеме за счет ухудшения понимаемости условная вершина с пометкой Y = 3 и вторая операторная вершина с пометкой z = 1 могут быть исключены.
Граф-схема алгоритма аналогичной структуры может быть построена для любого графа переходов автомата Мура. При этом в отличие от графа переходов такая граф-схема алгоритма всегда может быть планарной. Применение всего лишь одной промежуточной переменной при "хорошей" организации структуры делает использование граф-схем этого типа весьма привлекательным. Единственный недостаток, кроме громоздкости, такого типа структур (если умалчивание значений выходных переменных исключено) состоит в том, что так как в них связь между фрагментами осуществляется не непосредственно как в графах переходов, а по данным (значениям переменной Y), то визуальное обнаружение генерирующих контуров становится весьма затруднительным.
Из изложенного следует, что если в качестве языка общения по каким-либо причинам выбрана граф-схема алгоритма без внутренних обратных связей, то в этом случае целесообразно применять граф-схема алгоритмов с дешифратором многозначно закодированных состояний.
При использовании многозначного кодирования открывается весьма эффективная в изобразительном отношении дополнительная возможность обеспечения связи между компонентами алгоритма управления (в том числе, и при реализации параллельных процессов) за счет обмена десятичными значениями используемых при взаимодействии номеров состояний компонент (возможность взаимодействия по входным, выходным и дополнительно вводимым внутренним переменным сохраняется). Пусть, например, требуется, чтобы вторая компонента перешла из первого состояния в третье, а третья компонента - из четвертого состояния в пятое при условии, что первая компонента находится в шестом состоянии. Тогда без введения дополнительных переменных этот параллельный процесс весьма наглядно отражается фрагментом системы взаимосвязанных графов переходов, представленным на рис.20.
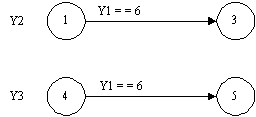
Рис. 20.
В [7] показано, что системы взаимосвязанных графов переходов обладают широкими изобразительными возможностями и, в частности, в явном виде отражают такие важные свойства сложных систем как параллелизм и иерархичность.
При этом отметим, что и один граф переходов являясь последовательным по состояниям обычно является параллельным по входам и выходам (например, графы переходов на рис.7 и 8).
В автоматах Мили, также как в автоматах Мура, могут использоваться различные виды кодирования состояний, однако, исходя из изложенного, рассмотрим только многозначное кодирование. На рис.8 [1] приведен граф переходов автомата Мили, реализующий счетный триггер при принятом варианте кодирования, а на рис.21 — соответствующая граф-схема алгоритма.
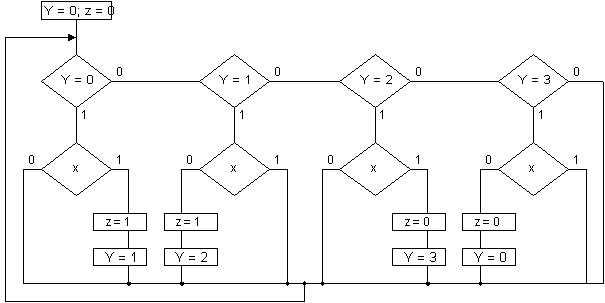
Рис. 21.
В этой граф-схеме могут быть исключены условная вершина с пометкой Y = 3 и вторые операторные вершины с пометками z = 1 и z = 0. Отличие этой граф-схемы от граф-схемы автомата Мура состоит в размещении слоя операторных вершин, помеченных значениями выходной переменной, не до дешифраторов значений входных переменных, а после них.
Второй пример реализации этого класса автоматов приведен на рис.22 для последовательностного одноразрядного сумматора (рис.10 [1]).
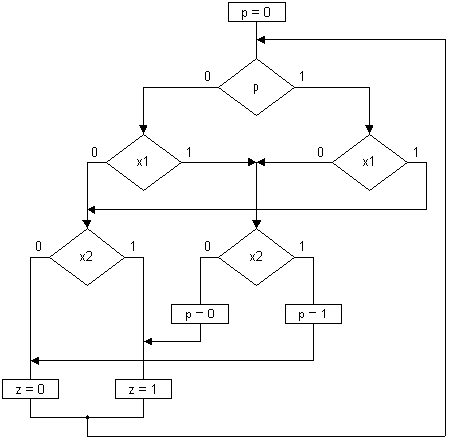
Рис. 22.
В этой граф-схеме для минимизации числа вершин слой значений выходной переменной z расположен после слоя со значениями следующего состояния P. Тело этой граф-схемы, состоящее всего лишь из девяти вершин, построено с помощью модификации метода Блоха, изложенной в [8].
На рис.23 изображено тело граф-схемы алгоритма, реализующей смешанный автомат с флагом, представленный на рис.11 [1].

Рис. 23.
Эта граф-схема является пятислойной: дешифратор состояний, формирование значений выходных переменных, реализация функций переходов, формирование значений флага, формирование следующего состояния. В приведенной граф-схеме переменная x1 определяет содержимое счетного триггера (еще одной компоненты алгоритма управления), который также управляется и от другого источника информации — кнопки. В этой граф-схеме в отличие от графа переходов противоречивость устранена ортогонализацией и используется булев признак T вместо неравенства t > D.
При этом необходимо отметить, что если при использовании системы взаимосвязанных графов переходов каждая компонента замкнута, то для граф-схем, реализуемых в программируемых логических контроллерах [9], замыкание выполняется для алгоритма управления в целом.