УНИВЕРСИТЕТ ИТМО
Кафедра «Технологии программирования»

Реализация алгоритмов логического управления программами на языке функциональных блоков

(c) 2000 А.А.Шалыто

3. Изоморфное построение функциональной схемы непосредственно по графу переходов

При использовании предлагаемого метода применяется граф переходов автомата Мура, вершины которого кодируются многозначно [8]. Этот граф переходов непосредственно и изоморфно реализуется одной из стандартных схем, рассмотренных ниже, которые строятся из традиционных логических элементов, логических (Л) и цифровых (Ц) мультиплексоров, а также преобразователей "десятичный код - двоичный код" (Д/В).

Логический мультиплексор имеет m логических управляющих входов, 2^m цифровых информационных входов и один цифровой выход, а цифровой мультиплексор - один цифровой управляющий и S цифровых информационных входов (S - число вершин в графе переходов (число состояний в автомате)), а также один цифровой выход.

На логические входы этих элементов подаются константы 0 и 1, а на цифровые - константы 0,1,2,...,S-1. При этом на цифровых выходах также формируются константы 0,1,2,...,S-1.

Обратим внимание на отличие этих элементов от элементов, традиционно называемых мультиплексорами, все входы и выходы которых являются логическими (двоичными) [11].

Предлагается использовать три варианта стандартных схем, первый из которых предполагает наличие логических мультиплексоров при m_i = 1, второй - при m_i = n_i, а третий - при m_i=k_i , где n_i - число переменных в булевых формулах, помечающих дуги, исходящие из i-й вершины графа переходов; k_i - число дуг, исходящих из i-й вершины.

В первом случае стандартную схему можно описать следующим образом. Комбинационная схема строится из традиционных логических элементов и реализует формулы, указанные на всех дугах графа переходов, за исключением петель. Выходы этой схемы подключены к управляющим входам логических мультиплексоров, а выходы подсхемы, состоящей из этих мультиплексоров, - к информационным входам первого цифрового мультиплексора, выход которого обратной связью соединен (для реализации петель в вершинах графа переходов) со своим управляющим входом и первыми, помеченными символом "0", информационными входами логических мультиплексорами (входы указанной подсхемы), а прямой связью - с управляющим входом второго цифрового мультиплексора, на информационные входы которого подаются десятичные эквиваленты наборов двоичных значений выходных переменных в соответствующих вершинах графа переходов. Выход второго цифрового мультиплексора подключен ко входам преобразователя, осуществляющего преобразование десятичного кода в значения двоичных выходных переменных. На остальные информационные входы логических мультиплексоров подаются десятичные эквиваленты номеров вершин, в которые осуществляются соответствующие переходы в графе переходов.

Оценим число элементов в такой схеме. Если число различных входных переменных в пометках дуг графа переходов равно N, то число инверторов в схеме не превысит N. Если общее число букв во всех булевых формулах на дугах (за исключением петель) графа переходов равно H, то число логических элементов, реализующих эти формулы, не превышает H - L, где L - число дуг (без учета петель) в графе переходов. Это объясняется тем, что для реализации i-й (i = 1,...,L) формулы из h_i букв требуется не более h_i - 1 двухвходовых элементов без учета инверсий, реализуемых в первом слое схемы. Так как каждый переход (дуга) в графе переходов реализуется одним логическим мультиплексором, то их общее число равно L. Так как в схему входят два цифровых мультиплексора и один преобразователь, общее число элементов в ней определяется соотношением:

Э₁ Ј N + (H - L) + L + 3 = N + H + 3.

Использование изложенного подхода позволяет реализовать граф переходов (рис.3) функциональной схемой (рис.4) из 11 элементов (Э₁ Ј 3 + 6 + 3 = 12).

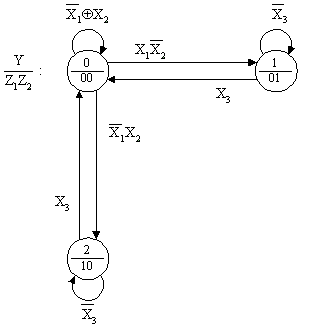
Рис. 3

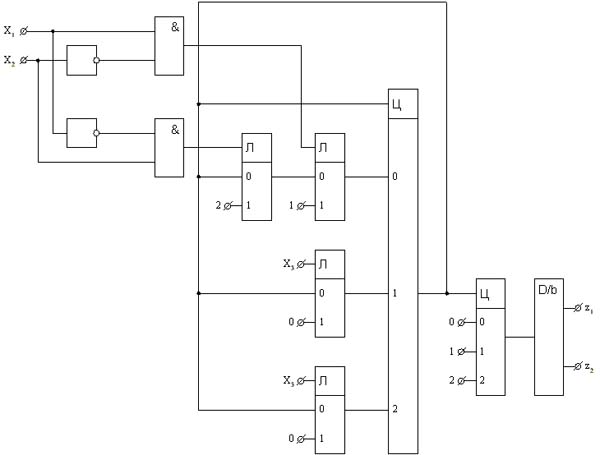
Рис. 4 (в натуральную величину)

Часть схемы этого типа, построенная из традиционных логических элементов, может быть упрощена, если противоречивость в графе переходов устранять не ортогонализацией как в рассмотренном примере, а расстановкой приоритетов [8]. При этом чем выше приоритет дуги, исходящей из j-й вершины графа переходов, тем ближе логический мультиплексор, соответствующий этой дуге, располагается к j-му информационному входу первого цифрового мультиплексора.

Вторая разновидность стандартных схем отличается от первой тем, что комбинационная схема из традиционных логических элементов не строится, а j-ый (j = 1,...,S) логический мультиплексор реализует все булевы формулы, помечающие дуги, исходящие из j-ой вершины графа переходов. Это удается осуществить в том случае, когда все указанные формулы взаимно ортогональны. Таким образом, число логических мультиплексоров в схеме равно S, а общее число элементов в схеме в этом случае

Э₂ = S + 3.

На рис.5 приведена схема из шести элементов, реализующая граф переходов, приведенный на рис.3.

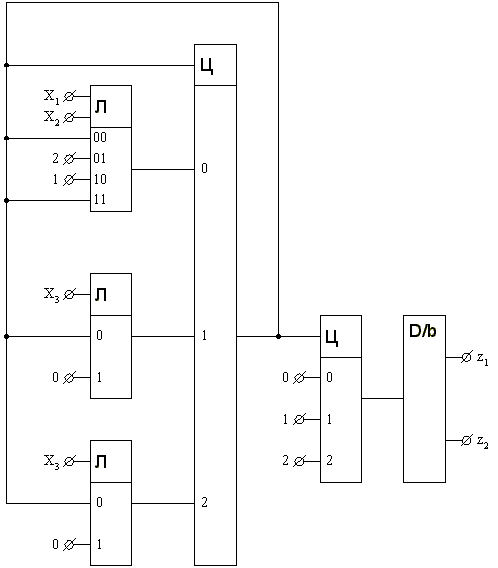
Рис. 5

Третий вариант стандартных схем является промежуточным между рассмотренными. Он содержит, как и вторая разновидность схем, S логических мультиплексоров, но в силу того что в этом случае число информационных входов i-го логического мультиплексора ограничено и равно M = 2^a , где a = ]log₂ k_i [, то приходится строить комбинационную схему из традиционных логических элементов так же, как в первом случае. Свободные информационные входы логических мультиплексоров подключаются к выходу первого цифрового мультиплексора, что обеспечивает сохранение состояний автомата. Число элементов в этом случае оценивается соотношением:

Э₃ Ј N + H - L + S + 3.

Граф переходов, представленный на рис.6, реализуется схемой третьего типа (рис.7) из 10 элементов (Э₃ Ј 4 + 7 - 4 + 3 + 3 = 13).

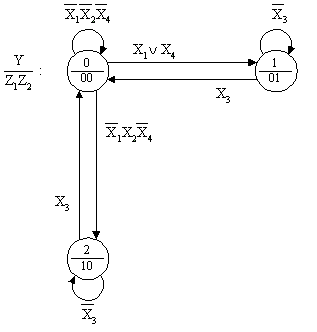
Рис. 6

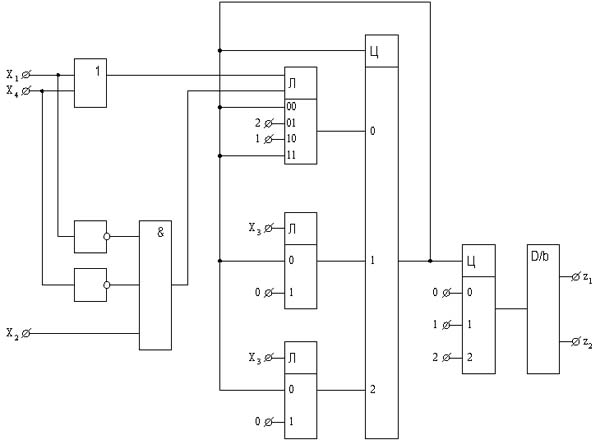
Рис. 7 (в натуральную величину)

Сравнивая рассмотренные типы схем, можно утверждать, что второй тип схем является наиболее однородным, а первый - наиболее просто моделируется программой на языке Си при использовании алгоритмической конструкции, соответствующей автомату Мура второго рода и построенной с помощью двух конструкций switch [8]. При этом каждой конструкции switch соответствует цифровой мультиплексор в схеме, а каждой конструкции if - соответствующий логический мультиплексор. Это позволяет моделировать программу, написанную на языке функциональных блоков, изоморфной программой на широко распространенном алгоритмическом языке высокого уровня.

Изложенный метод построения функциональных схем позволяет предложить новый подход к их сертификационному тестированию, которое предлагается проводить в два этапа. На первом этапе наблюдая за значениями одной внутренней переменной Y, кодирующей состояния автомата, в динамике по графу переходов проверяется правильность реализации программой каждого из переходов в графе, а на втором - в статике по графу переходов анализируется правильность формирования программой значений выходных переменных, указанных в каждой вершине графа.