Определение 1. Граф переходов, в котором в каждой вершине явно указаны значения каждой выходной переменной, назовем графом переходов автомата Мура с явным заданием значений всех выходных переменных.
В этом случае значения выходов соответствуют номеру вершины и не зависят от предыстории. По этой причине такой граф переходов просто понимается и в него легко вносятся изменения.
Определение 2. Граф переходов, в котором в вершинах, кроме явно определенных значений одних переменных, применяются также неявно, но однозначно определенные значения других переменных, назовем графом переходов автомата Мура с неявным заданием значений выходных переменных.
Неявное задание переменной в вершине отображается прочерком, который в данном случае может быть заменен только одним значением булевой переменной. Эта переменная в рассматриваемой вершине сохраняет то значение, которое присваивается ей во всех "смежных" с ней вершинах. Связь между двумя вершинами может быть непосредственной с помощью заходящей в вершину дуги или транзитной через другие вершины, в которых вместо значений этой переменной используются проверки.
Графы переходов этого типа читаются несколько хуже, чем графы переходов автоматов Мура первого типа, однако их целесообразно использовать для сокращения объема памяти программ, изоморфно отражающих графы переходов автоматов Мура. Графы переходов этого класса могут быть изображены таким образом, что в нем в каждой вершине в явном виде указаны значения каждой выходной переменной, а неизменяющиеся относительно "смежных" вершин значения этих переменных отмечаются перечеркиванием.
Определение 3. Граф переходов, в котором в вершинах, кроме явно определенных значений одних переменных, используются также неявно и неоднозначно заданные значения других переменных, назовем графом переходов автомата Мура с неоднозначным заданием значений выходных переменных.
Графы переходов этого класса могут содержать для одной и той же задачи меньшее число вершин, чем графы переходов автоматов Мура двух других указанных выше разновидностей, так как в этом случае в вершине вместо одного значения умалчиваемой переменной могут формироваться различные значения той же переменной, что порождает в этой вершине различные наборы значений выходных переменных и обеспечивает эквивалентность одной такой вершины нескольким, полностью определенным.
Это преимущество с точки зрения компактности описания и сокращения длины программы порождает одновременно и главный недостаток графов переходов этого типа — трудность их чтения и понимания. Именно по этой причине такие графы переходов не рекомендуется использовать в качестве языка общения.
Спецификацию задач рассматриваемого класса целесообразно производить с помощью двух первых моделей графов переходов автоматов Мура, а в случае использования для спецификации ГСА1 последнюю целесообразно преобразовать к одной из этих моделей графов переходов.
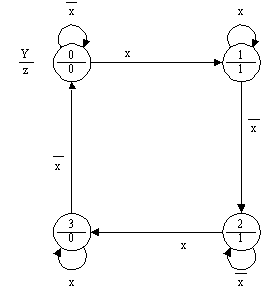
Это, естественно, не исключает применение графов переходов для других классов автоматов. Аналогичная классификация может быть предложена для графов переходов автоматов Мили, в которых значения выходных переменных формируются не в вершинах графов переходов, а на дугах [36]. Во многих задачах логического управления переход от модели автомата Мура к модели автомата Мили не уменьшает числа состояний (вершин графа переходов). На рис.7 в качестве примера приведен граф переходов автомата Мура, реализующий счетный триггер, а на рис.8 эта же задача описана с помощью графа переходов автомата Мили.

Рис. 7.
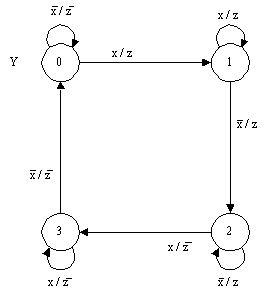
Рис. 8.
В других случаях переход от графа переходов автомата Мура или графа переходов автомата без выходного преобразователя к графу переходов автомата Мили позволяет сократить число вершин. На рис.9 приведен граф переходов автомата без выходного преобразователя с четырьмя вершинами, реализующий последовательностный одноразрядный сумматор, а на рис.10 этот алгоритм описан графом переходов автомата Мили с двумя вершинами.
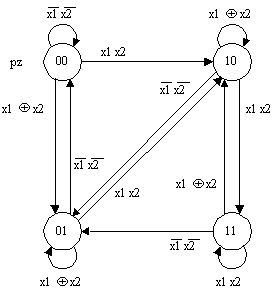
Рис. 9.
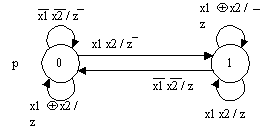
Рис. 10.
При этом необходимо отметить, что если для автоматов Мура и автоматов без выходного преобразователя с однозначным заданием значений выходов число состояний равно числу комбинаций этих значений (среди которых учитываются повторяющиеся), а для автоматов, в которых все комбинации различны, равно числу различных комбинаций, то уже для автоматов этих классов с неоднозначным их заданием понятие "состояние" становится менее связанным со значениями выходов и поэтому становится более абстрактным и менее понятным.
Это положение усугубляется для автоматов Мили, а для автоматов этого класса с неоднозначными значениями выходов в [37] вместо понятия "состояние" было введено понятие "ситуация", а вместо термина "граф переходов" - термин "граф переключений". Однако несмотря на то, что граф переключений может содержать меньшее число вершин, чем эквивалентный граф переходов, применение графов переключений в качестве языка общения нецелесообразно ввиду сложности их понимания.
Аналогичная ситуация с числом состояний из-за умолчаний значений переменных может иметь место и для такого типа автоматов как смешанные автоматы — "автоматы без выходного преобразователя-Мили (СА1)" и "автоматы Мура-Мили (СА2)", а также для автоматов всех перечисленных классов с флагами, в которых одна и та же переменная может использоваться в одном графе переходов как в качестве входной, так и выходной переменной.
В качестве флага в ряде случаев могут использоваться переменные, если они находятся в ячейках памяти, значения которых проверяются автоматом и могут быть изменены не только внешним относительно рассматриваемого автомата источником информации, например кнопкой, но и собственно автоматом. В графе переходов СА2 (рис.11) в качестве флага используется переменная x1, значения которой, сохраняемые во внешней относительно автомата битовой ячейке памяти, могут быть изменены в устойчивых состояниях автомата кнопкой или собственно автоматом на переходе 0-2, инициируемом входной переменной x0. Значения переменной x1 не только формируются автоматом, но и проверяются им на переходах 0-1 и 2-3.
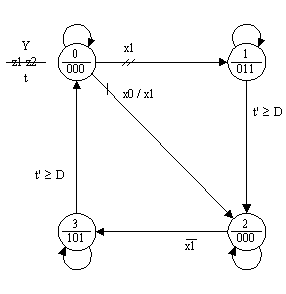
Рис. 11.
Более типично использование флагов как дополнительно введенных переменных, которые воздействуют на ячейки памяти, содержимое которых не может быть изменено от других источников информации. В случае, когда флаги вводятся в автомат без выходного преобразователя, то эти ячейки могут рассматриваться как принадлежность автомата наряду с ячейками, сохраняющими значения переменных, различающих состояния.
Для автоматов Мура, Мили и смешанных автоматов флагами являются дополнительно вводимые переменные F, значения которых запоминаются в ячейках памяти, внешних относительно рассматриваемого автомата. Если при использовании многозначного кодирования состояний автомата любой сложности, принадлежащих этим классам, достаточно иметь в автомате только одну промежуточную переменную, то при введении флагов во внешней относительно автомата среде появляются дополнительные ячейки памяти, в том числе и многозначные. При этом номер следующего состояния определяется не только номером рассматриваемого состояния и входным воздействием, как это имеет место в автоматах без флагов, но зависит от предыстории.
Таким образом, для таких автоматов не только значения выходов, но и значения состояний могут зависеть и изменяться от предыстории, что, естественно, резко усложняет их чтение.
На рис.12 приведен не содержащий ни одной устойчивой вершины граф переходов автомата Мура с десятью вершинами. Число вершин в графе переходов автомата Мура удается сократить до семи за счет введения двоичного флага F1, формируемого и проверяемого автоматом, и неоднозначности значений флага в некоторых вершинах графа переходов (рис.13). Дальнейшее сокращение числа вершин в графе переходов автомата Мура обеспечивается введением дополнительного многозначного флага F2 и использованием умолчаний его значений (рис.14).
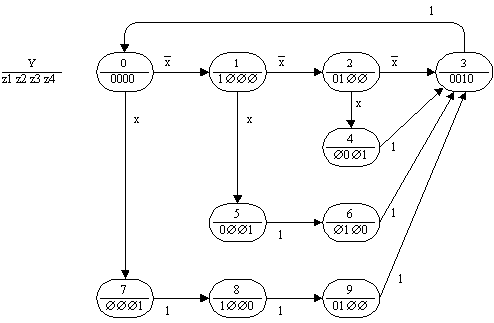
Рис. 12.
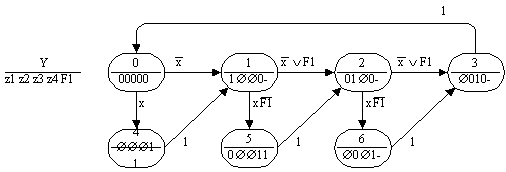
Рис. 13.
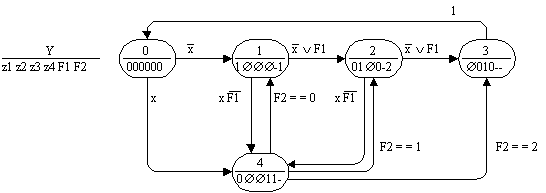
Рис. 14.
Методы построения понимаемых графов переходов по граф-схемам алгоритмов и понимаемых граф-схем алгоритмов по графам переходов, а также методы программирования рассматриваемых моделей в базисе языков различных уровней рассматриваются во второй части работы.